Uitgelegd: De stelling van Pythagoras
De Stelling van Pythagoras is een van de meest beroemde en fundamentele stellingen in de wiskunde. Deze stelling, die haar naam ontleent aan de oude Griekse wiskundige Pythagoras, heeft de basis gelegd voor tal van wiskundige concepten en heeft een enorme invloed gehad op de wetenschap en technologie door de eeuwen heen. In dit artikel zullen we de essentie van de stelling van Pythagoras bespreken, haar geschiedenis verkennen en enkele van haar toepassingen onderzoeken.
Wat is de stelling van Pythagoras?
De Stelling van Pythagoras in een Notendop
De Stelling van Pythagoras is een wiskundige uitspraak die betrekking heeft op rechthoekige driehoeken, dat wil zeggen driehoeken met één rechte hoek (90 graden).
De stelling luidt als volgt
In een rechthoekige driehoek is het kwadraat van de lengte van de hypotenusa gelijk aan de som van de kwadraten van de lengtes van de twee rechthoekszijden.
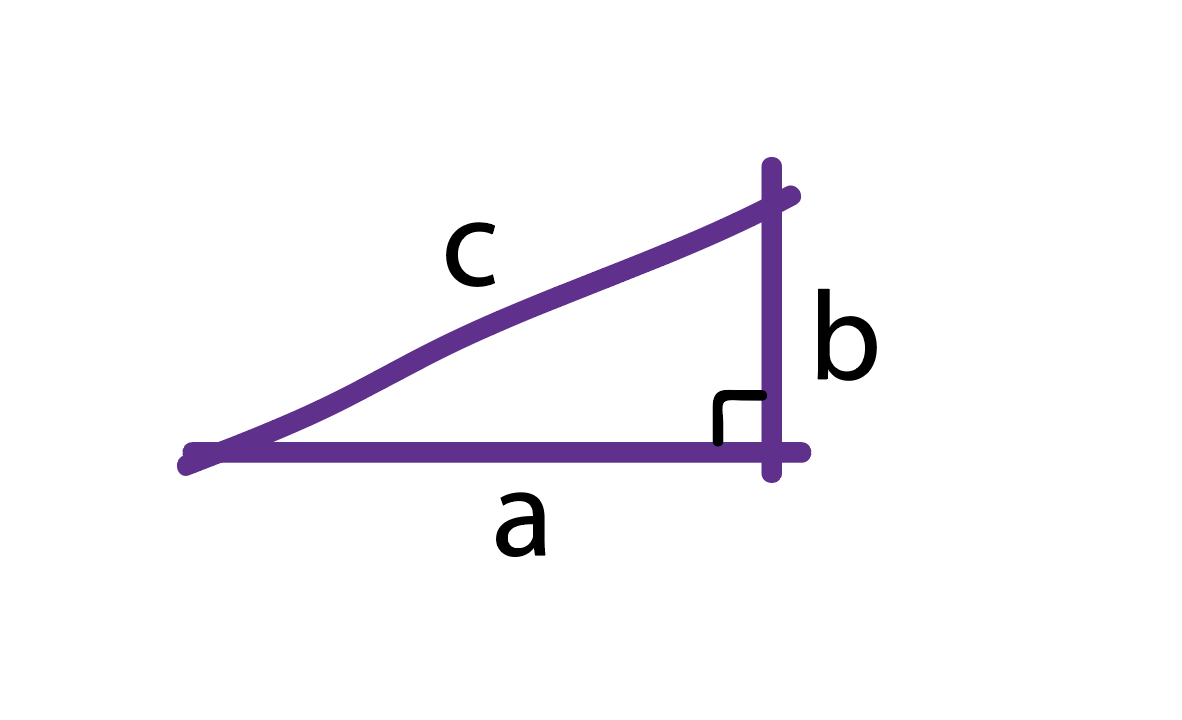
Dit kan als volgt worden uitgedrukt in een wiskundige vergelijking:
a2+b2=c2
Hierbij staat 'c' voor de lengte van de hypotenusa (de schuine zijde tegenover de rechte hoek), en 'a' en 'b' staan voor de lengtes van de rechthoekszijden.
Wanneer je de lengte van a en b weet, dan kan je de lengte van c berekenen:
Voorbeeld
Als zijde a een lengte van 3 heeft en b een lengte van 4 dan vullen we dit in in de formule:
32+42 = c2
wat gelijk staat aan
(3x3)+(4x4) = (cxc)
wat gelijk staat aan:
9+16 = c2
wat gelijk staat aan:
25 = c2
om c te kunnnen berekenen moeten we de wortel trekken uit 25:
c = √25
wat gelijk staat aan:
c = 5
Video
In onderstaande video wordt de Stelling van Pythagoras heel duidelijk uitgelegd:
Geschiedenis
De Geschiedenis van de Stelling van Pythagoras
De stelling is vernoemd naar Pythagoras, een Griekse wiskundige en filosoof die leefde rond 570-495 v.Chr. Hoewel Pythagoras zelf niet wordt beschouwd als de ontdekker van de stelling, wordt hij wel vaak geassocieerd met de ontwikkeling ervan. Er zijn aanwijzingen dat de Babyloniërs en oude Egyptenaren al eerder bekend waren met deze stelling, maar Pythagoras en zijn school bestudeerden het grondiger en formaliseerden het.
Toepassing
Toepassingen van de Stelling van Pythagoras
De Stelling van Pythagoras heeft talloze praktische toepassingen in de wiskunde, natuurkunde, techniek en vele andere wetenschappelijke disciplines. Enkele voorbeelden zijn:
-
Afstandsformule: De stelling wordt vaak gebruikt om de afstand tussen twee punten in een coördinatensysteem te berekenen.
-
Bouw en architectuur: Architecten gebruiken de stelling om hoeken te berekenen en constructies te ontwerpen.
-
Navigatie: Zeelieden en piloten passen de stelling toe om hun positie en koers te bepalen.
-
Wetenschap: In de fysica wordt de stelling gebruikt om krachten en bewegingen te analyseren.
-
Computergraphics: Bij het renderen van 3D-objecten worden de coördinaten van punten berekend met behulp van de stelling.
-
Gevorderde wiskunde: De stelling is de basis voor veel geavanceerde wiskundige concepten, zoals de euclidische meetkunde en de stelling van Pythagoras in niet-euclidische meetkunde.
Kortom, de Stelling van Pythagoras is niet alleen een wiskundige stelling, maar ook een krachtig instrument dat de basis vormt voor tal van praktische toepassingen in ons dagelijks leven en in de wetenschap. Haar eenvoud en elegantie hebben haar een blijvende plaats gegeven in de wereld van de wiskunde en daarbuiten.
Ik schrijf over studies en studeren